Option A is correct. Only asymmetric encryption actually uses a separate public and private key pair, like RSA or ECC. Symmetric (B) always just has one secret shared between both sides. Pretty sure exam reports confirm this logic but open to debate if someone has seen it otherwise.
Yeah, that's A. FlexVPN active/active mode is great because you can set up several routers or VRFs as hubs, which DMVPN can't match. DMVPN does active/standby but not real multi-hub active. If you need scale and redundancy with more than one hub, FlexVPN is the way to go.
Seen this type on several practice sets, the official guide spells it out. RSA (C) is always the asymmetric one listed here, while RC4, AES, and 3DES are symmetric. If anyone saw a twist on exam let me know but pretty sure it stays this way.
C for sure. RSA is the only one that's actually asymmetric, the rest (RC4, AES, 3DES) are symmetric block or stream ciphers. Pretty common to see questions trying to trip you up with 3DES or AES here, but it's always RSA for asymmetric. Any objections?
DRAG DROP [Network Security] Drag and drop the VPN functions from the left onto the description on the right.

This order looks solid to me: SHA-1 for integrity, ISAKMP for IKE SAs, AES does confidentiality, RSA gives authentication. Pretty standard VPN roles per Cisco docs. If anyone sees a gotcha here let me know but I think this covers it.
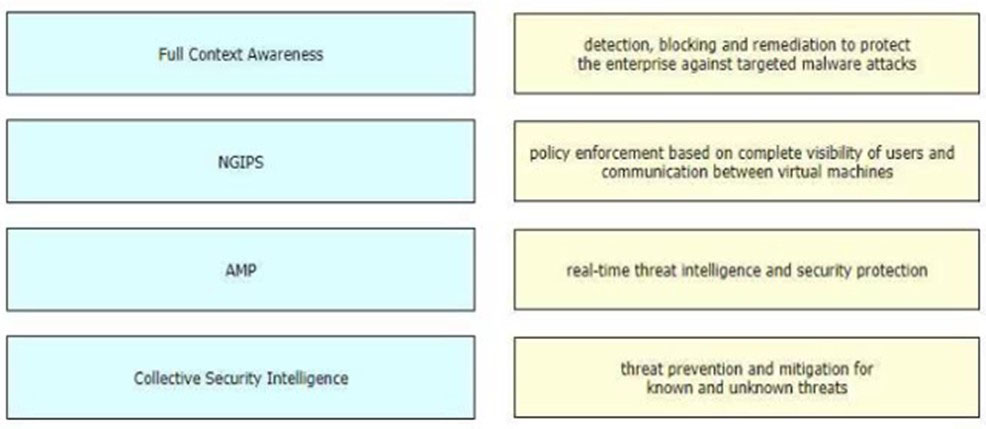
DRAG DROP [Security Concepts] Drag and drop the features of Cisco ASA with Firepower from the left onto the benefits on the right.
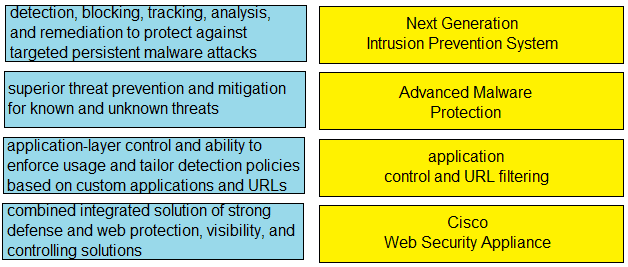
DRAG DROP [Security Concepts] Drag and drop the capabilities from the left onto the correct technologies on the right.
Next Generation Intrusion Prevention System matches with "superior threat prevention and mitigation for known and unknown threats," while Advanced Malware Protection is about "detection, blocking, tracking, analysis, and remediation." App-layer control lines up with "application control and URL filtering," and WSA is the one described as a "combined integrated solution." I think this is right, since AMP's retrospective functions get overlooked easily-NGIPS sounds similar but it's more about active prevention than after-the-fact tracking. Anyone see it differently?
This matches typical Cisco exam mappings. NGIPS gets "superior threat prevention," AMP is "detection, blocking, tracking, analysis, and remediation," app control/URL filtering is the application-layer control one, and WSA is the integrated web protection. Official study guide has this breakdown if you want to double-check.
NGIPS gets "superior threat prevention and mitigation for known and unknown threats" since that's its main purpose. AMP goes with "detection, blocking, tracking, analysis, and remediation" because that's the retrospective angle. Seen this on study guides so pretty confident but let me know if I missed something.
AMP → detection, blocking, tracking, analysis, and remediation
App control/URL filtering → application-layer control on apps and URLs
WSA → combined web protection solution.
Not seeing a reason to swap AMP and NGIPS here-the keywords match the specific tech well. NGIPS is all about broad threat prevention, while AMP does tracking/analysis/remediation (that after-the-fact stuff). Sometimes WSA throws people off but it's definitely the all-in-one web defense. Pretty confident but open if you spot something off.