The simulation requires selecting the most appropriate regression model based on the provided information. A primary metric for evaluating a regression model's goodness-of-fit is the R-squared (R²) value. This metric represents the proportion of the variance in the dependent variable (sales) that is predictable from the independent variables. A higher R² value indicates a better-fitting model.

Comparing the R² values shown in the titles of the four plots:

• Linear regression: R² = 0.8
• Lasso regression: R² = 0.62
• Quantile regression: R² = 0.6
• Ridge regression: R² = 0.5

The Linear regression model has the highest R² (0.8), explaining 80% of the variance. This is significantly higher than the other models, making it the most appropriate choice for this analysis.

(Note: Part 2 of the simulation, which requires identifying a statistically significant variable, cannot be completed as the "summary output and variable table" was not provided.)

James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An Introduction to Statistical Learning: with Applications in R. Springer.

Reference: Chapter 3, "Linear Regression," Section 3.1.3, "Assessing the Accuracy of the Model."

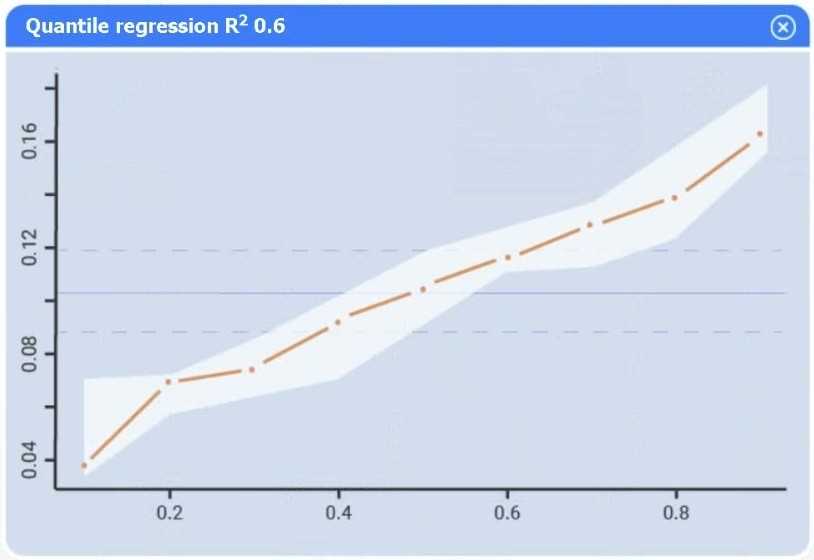
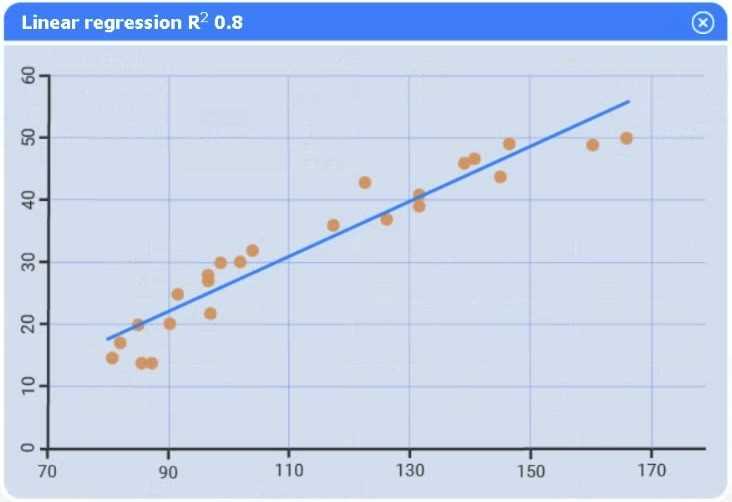
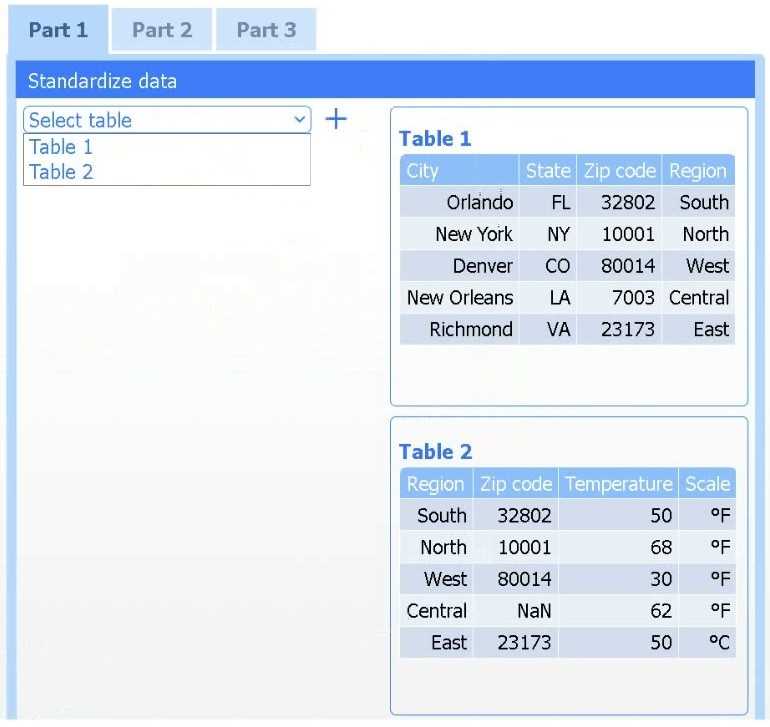
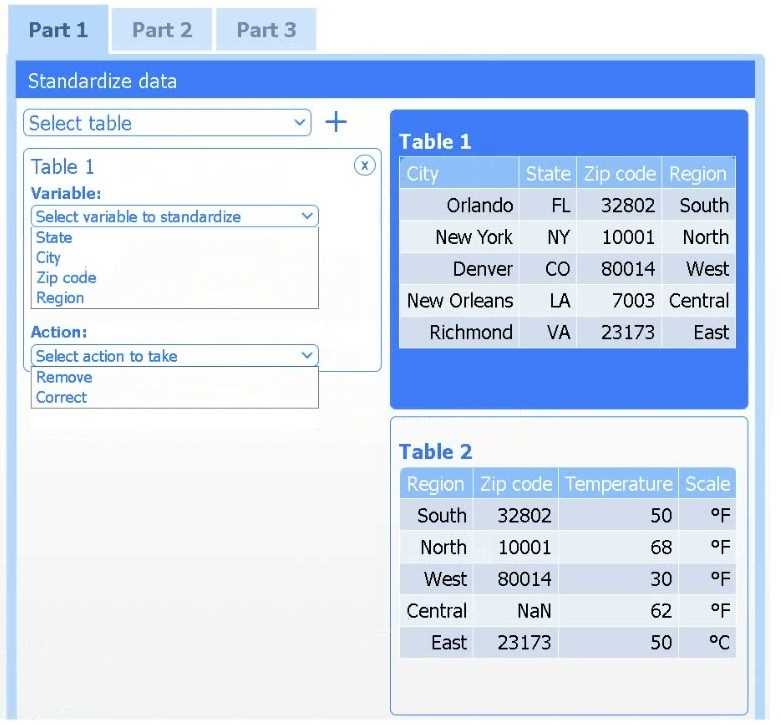
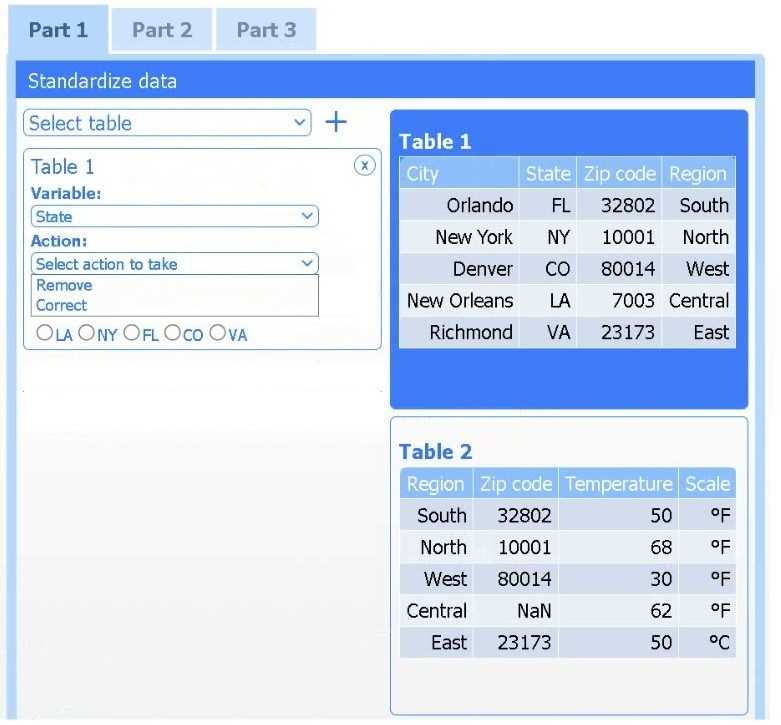
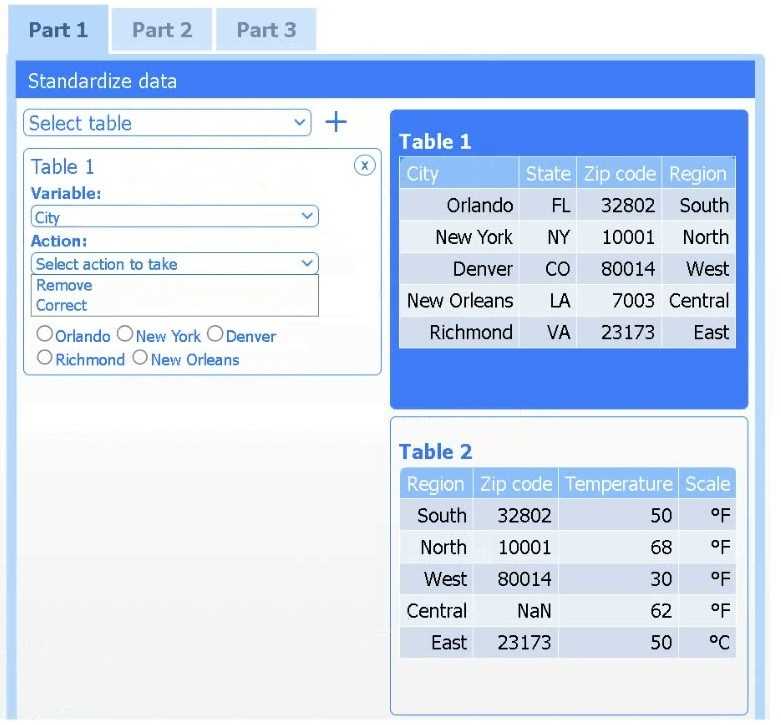
Detail: This section explains the R-squared (R²) statistic, or coefficient of determination, as a key measure of the linear relationship between the response and predictors. It is defined as the "proportion of variance explained" and ranges from 0 to 1, with higher values indicating a better fit.

DOI: https://doi.org/10.1007/978-1-4614-7138-7_3

Draper, N. R., & Smith, H. (1998). Applied Regression Analysis (3rd ed.). Wiley.

Reference: Chapter 2, "Checking the Regression Model," Section 2.10, "The Coefficient of Determination, R²."

Detail: This section formally defines R² and discusses its use in "evaluating the quality of the fit." It establishes the principle that among several candidate models, the one with the higher R² (adjusted for the number of predictors) is generally preferred.

DOI: https://doi.org/10.1002/9781118625590

Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction (2nd ed.). Springer.

Reference: Chapter 3, "Linear Methods for Regression," Section 3.2, "Linear Regression Models and Least Squares."

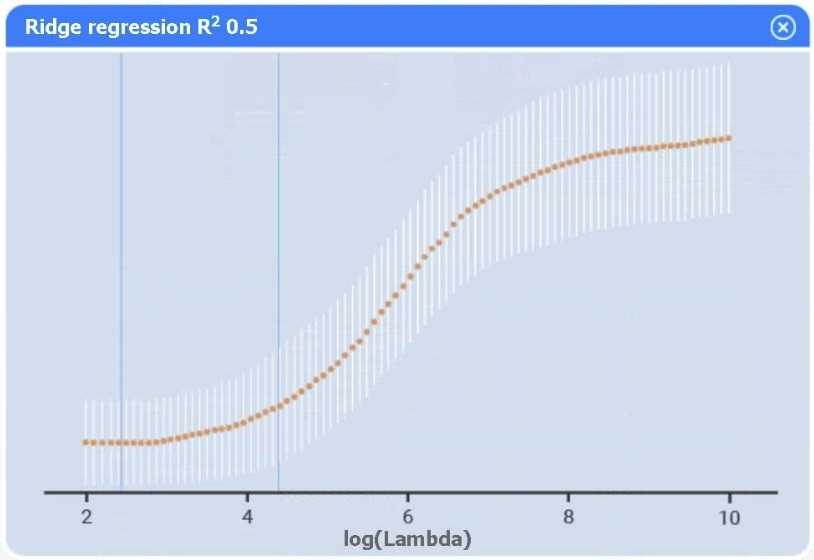
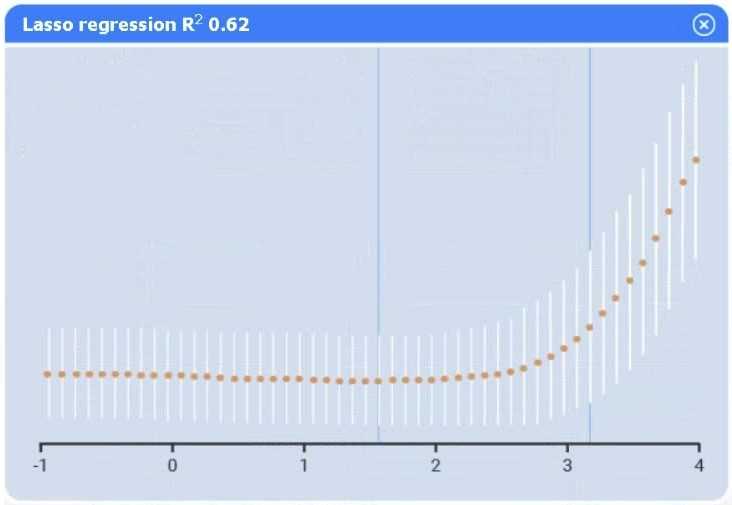
Detail: This foundational text discusses model assessment and selection. It contrasts simple linear regression with more complex methods like Ridge (Section 3.4.3) and Lasso (Section 3.4.2), noting that while these methods are useful for high-dimensional data or multicollinearity, the base R² remains a primary metric for comparing overall model fit.

DOI: https://doi.org/10.1007/978-0-387-84858-7

To prepare the data, you must first standardize the disparate values. The '50 °C' in Table 2 must be converted to 122 °F to match the '°F' scale of all other temperature data. The 'NaN' (Not a Number) zip code for the 'Central' region must be corrected to '7003' by referencing Table 1.

In Part 2, Data matching (a database Join) is the correct method to combine tables by adding columns from one to another based on a shared key. A 'Union' would incorrectly stack rows. Zip code is the correct join variable as it is a unique identifier (a primary/foreign key) for each location, whereas 'Region' is too general.

In Part 3, the Choropleth Map is the most appropriate visualization. After standardizing, the data includes high-temperature outliers (e.g., 122°F for Virginia). The choropleth map correctly plots the temperature data by state/region (e.g., VA as '75°F+', NY as '60-75°F'), directly answering the client's request to see which regions have high temperatures.

On Data Standardization (Unit Conversion & Missing Data):

Wickham, H. (2014). Tidy Data. Journal of Statistical Software, 59(10), 1-23. (Section 3.3 discusses standardizing variables, which includes converting units for valid comparison, and Section 3.2 addresses missing values, such as 'NaN').

DOI: https://doi.org/10.18637/jss.v059.i10

On Merging Data (Join vs. Union):

MIT OpenCourseWare. (2008). 6.830 Database Systems, Lecture 3: Relational Algebra. (This lecture material formally defines the 'Join' (Data matching) operation as the method for combining tables based on common attributes, contrasting it with 'Union', which requires tables to have identical schemas and appends rows).

Reference: See "Join" and "Union" operators in the Relational Algebra lecture notes.

On Visualization (Choropleth Maps):

The University of Chicago. (n.d.). Geographic Data: Visualization. (This resource from the UChicago Library Data Services explains that choropleth maps are used to "show data aggregated for geographic regions... by coloring those regions," making them ideal for visualizing data like temperature by state or region, as requested by the client).

Reference: Section on "Choropleth Maps."

The model must be retrained every 24 hours so that today’s pricing reflects yesterday’s sales. Because this retraining occurs on a fixed, short schedule, the dominant constraint is how long it takes to complete each training run; excessive training time would delay or prevent daily price updates. The other activities (initial development, deployment automation, and ingesting the previous day’s sales, which are already stored) occur once or require far fewer resources than the recurrent training step.

A. Deployment time – Once a CI/CD pipeline is built, pushing the new model is fast and usually automated; it runs after training completes.

C. Development time – Model design and coding are mostly one-off efforts completed before daily operations begin.

D. Data collection time – Yesterday’s sales data already reside in transactional systems; extraction is trivial compared with compute-intensive retraining.

1. Google Cloud

“MLOps: Continuous Delivery and Automation Pipelines in Machine Learning

” v2

2020

p.4 §“Training frequency and compute cost”.

2. AWS

“Machine Learning Operations (MLOps) Fundamentals

” whitepaper

2021

p.9 §“Automated Model Retraining and Scheduling”.

3. MIT OpenCourseWare

6.S897 “Machine Learning Production Systems

” Lecture 4 slides

slide 12 “Time-boxed retraining as the main operational bottleneck”.

4. Stanford CS329S “Machine Learning Systems Design

” Spring 2022 notes

Week 5 §“Retraining cadence and resource constraints”.

Scheduling problems fundamentally involve allocating limited resources to tasks over time to achieve a specific goal, such as minimizing total completion time or maximizing output. This structure is defined by an objective function (the goal) and a set of constraints (the rules and limitations, like resource availability or task dependencies). Constrained optimization is the mathematical and computational framework designed explicitly to find the best solution (optimum) for an objective function subject to a given set of constraints. Therefore, it is the most appropriate modeling tool for solving scheduling problems.

A. One-armed bandit: This is a reinforcement learning model for balancing exploration and exploitation, not for solving problems with the fixed, complex constraints typical of scheduling.

C. Decision tree: This is a supervised learning model for classification or regression. It predicts an outcome based on input features but does not construct an optimal schedule.

D. Gradient descent: This is an optimization algorithm used to find the minimum of a function, primarily for training machine learning models, not for modeling combinatorial scheduling problems.

1. University Courseware: Bertsimas

D.

& Freund

R. M. (2004). 15.053 Optimization Methods in Business Analytics

Fall 2004. Massachusetts Institute of Technology: MIT OpenCourseWare. In Lecture 5

"Integer Programming Formulations

" scheduling problems (e.g.

the job shop scheduling problem) are presented as classic examples that are modeled and solved using integer programming

a specific class of constrained optimization.

2. University Courseware: Liang

P.

& Sadigh

D. (2021). CS221: Artificial Intelligence: Principles and Techniques

Autumn 2021. Stanford University. Lecture 6

"Constraint Satisfaction Problems

" introduces scheduling as a canonical example of a CSP

where variables (e.g.

start times of tasks) must be assigned values that satisfy a set of constraints. CSPs are a form of constrained optimization.

3. Academic Publication: Pinedo

M. L. (2016). Scheduling: Theory

Algorithms

and Systems (5th ed.). Springer. In Chapter 2

"Framework and Classification

" scheduling problems are formally defined in terms of their objective functions and constraints

which is the core structure of a constrained optimization model.

A memory constraint error in a distributed computing environment signifies that the collective RAM of the cluster's nodes is insufficient for the model's processing demands. The most direct solution is to scale the cluster horizontally by adding more nodes. This action increases the total aggregate memory available to the distributed system. The workload can then be partitioned and distributed across a larger number of machines, reducing the memory load on each individual node and resolving the overall memory bottleneck. This is a fundamental principle of scaling distributed data processing frameworks.

A. Converting an on-premises deployment to a containerized deployment packages the application but does not inherently increase the physical memory of the host machines.

B. Migrating to a cloud deployment only provides the potential for scaling; the direct action that resolves the error is provisioning more or larger resources (nodes), not the migration itself.

C. Moving model processing to an edge deployment would likely worsen the problem, as edge devices are typically far more constrained in memory and processing power than cluster nodes.

1. Zaharia

M.

Chowdhury

M.

Franklin

M. J.

Shenker

S.

& Stoica

I. (2012). Resilient distributed datasets: A fault-tolerant abstraction for in-memory cluster computing. In Proceedings of the 9th USENIX conference on Networked Systems Design and Implementation (NSDI'12). USENIX Association. Section 3.1

"RDD Abstraction

" describes how datasets are partitioned across machines in a cluster. Increasing the number of machines (nodes) allows for a greater distribution of these partitions

thus increasing the total memory capacity for the dataset.

2. MIT OpenCourseWare. (2020). 6.824 Distributed Systems

Spring 2020. Lecture 3: GFS. The lecture discusses how Google File System (and by extension

other distributed systems like MapReduce) achieves scalability for large datasets by distributing data and computation across a large number of commodity machines (nodes). Adding nodes is the primary mechanism for scaling.

3. Armbrust

M.

et al. (2015). Spark SQL: Relational Data Processing in Spark. In Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data (SIGMOD '15). Association for Computing Machinery

New York

NY

USA

1383–1394. Section 2

"Programming Model

" explains how Spark's distributed execution allows it to scale "by adding more machines to a cluster." This directly addresses resource constraints like memory. DOI: https://doi.org/10.1145/2723372.2742797

The Normal distribution is the most appropriate model for representing the actual arrival times of a bus on a fixed schedule. The scheduled arrival time acts as the mean (average) of the distribution. Actual arrivals will naturally vary due to factors like traffic, weather, and passenger load. These variations cause most arrival times to cluster closely around the scheduled time, with fewer arrivals occurring significantly early or late. This symmetric, bell-shaped clustering around a central value is the defining characteristic of a Normal distribution, making it the most effective model for this scenario.

A. Binomial: This distribution models the number of successes in a set number of discrete trials (e.g., heads in 10 coin flips), not a continuous variable like time.

B. Exponential: This distribution models the time between independent, random events (e.g., time until the next customer arrives), not deviations from a scheduled event.

D. Poisson: This distribution models the count of events occurring in a fixed interval (e.g., number of buses arriving in an hour), not the precise arrival time of a single bus.

---

1. MIT OpenCourseWare. (2014). 18.05 Introduction to Probability and Statistics

Spring 2014. Lecture 13: Central Limit Theorem. Massachusetts Institute of Technology. The notes describe the Normal distribution as a model for phenomena resulting from the sum of many small

independent random effects

which accurately describes the various factors (traffic

passengers

etc.) causing deviations in a bus's scheduled arrival time. (See Section 2

"The Bell Curve").

2. Stanford University. (2023). CS109: Probability for Computer Scientists

Lecture Notes 12: Normal Distribution. The lecture notes explain that the Normal distribution is often used to model real-world continuous variables where values cluster around a mean

such as measurement errors. The deviation of a bus's arrival time from its schedule is a form of measurement error. (See "Normal Random Variable" section).

3. University of California

Berkeley. (2021). STAT 20: Introduction to Probability and Statistics

Lecture 17: The Normal Distribution. The course material explicitly states that the Normal distribution is a suitable model for continuous random variables where the data is expected to be symmetric and centered around a mean

which is the expected pattern for bus arrivals relative to a schedule. (See "Properties of the Normal Curve").

The question describes a univariate time series forecasting problem where future values of a variable (copper price) are to be predicted based solely on its own past values. An autoregressive (AR) model is the most appropriate technique for this scenario. An AR model is a regression model that uses the dependent relationship between an observation and a number of lagged observations (i.e., its own past values) to forecast future values. This directly matches the data scientist's approach of using only the historical daily price of copper as input.

B. Moving average: This is a calculation to analyze data points by creating a series of averages of different subsets of the full data set. It is primarily used for smoothing data to identify trends, not as a direct forecasting model in this context.

C. Dynamic time warping: This is an algorithm used to measure the similarity between two temporal sequences, which may vary in speed. It is applied in classification or clustering, not for forecasting a single time series.

D. Relative strength: This is a specific technical momentum indicator used in financial analysis to measure the magnitude of recent price changes. It is a derived metric, not a general forecasting technique for the price itself.

1. Pennsylvania State University

STAT 510: Applied Time Series Analysis. (n.d.). Lesson 1.2: The AR Model. Eberly College of Science. Retrieved from https://online.stat.psu.edu/stat510/lesson/1/1.2. The courseware defines: "An autoregressive model is when a value from a time series is regressed on previous values from that same time series." This directly supports the choice of Autoregressive for the described task.

2. Box

G. E. P.

Jenkins

G. M.

Reinsel

G. C.

& Ljung

G. M. (2015). Time Series Analysis: Forecasting and Control (5th ed.). John Wiley & Sons. In Chapter 3

"Linear Stationary Models

" Section 3.1.1

"The Autoregressive Process

" the text formally defines the AR(p) model where the current value of the process is expressed as a finite

linear aggregate of previous values of the process and a random shock.

3. Hyndman

R. J.

& Athanasopoulos

G. (2018). Forecasting: Principles and Practice (2nd ed.). OTexts. In Chapter 8

Section 8.3

"Autoregressive (AR) models

" it is stated

"In an autoregression model

we forecast the variable of interest using a linear combination of past values of the variable."

4. Berndt

D. J.

& Clifford

J. (1994). Using dynamic time warping to find patterns in time series. In KDD workshop (Vol. 10

No. 16

pp. 359-370). This foundational paper describes DTW as a method for providing "a distance measure between two time series" (p. 360)

establishing its role in similarity measurement rather than forecasting.

The term "deep" in deep learning directly refers to the architecture of the neural network having multiple layers between the input and output layers. These intermediate layers are known as hidden layers. A shallow neural network might have only one hidden layer, whereas a deep neural network is characterized by having many hidden layers stacked upon each other. Each hidden layer learns to represent the data at a different level of abstraction, allowing the model to learn complex patterns and hierarchical features. The number of hidden layers determines the network's depth.

A. Convolution: This is a specific type of layer, common in deep learning for tasks like image recognition, but it is not the general term for the layers that create depth.

B. Dropout: This is a regularization technique applied to layers to prevent overfitting by randomly ignoring some neurons during training; it does not define the network's depth.

C. Pooling: This is a specific type of layer used for down-sampling feature maps, typically in conjunction with convolutional layers, not the fundamental component of depth.

---

1. LeCun

Y.

Bengio

Y.

& Hinton

G. (2015). Deep learning. Nature

521(7553)

436–444.

Page 436

Column 1

Paragraph 2: "Deep learning allows computational models that are composed of multiple processing layers to learn representations of data with multiple levels of abstraction." These "multiple processing layers" are the hidden layers that constitute the model's depth.

DOI: https://doi.org/10.1038/nature14539

2. Goodfellow

I.

Bengio

Y.

& Courville

A. (2016). Deep Learning. MIT Press.

Chapter 6

Deep Feedforward Networks

Section 6.4

Page 195: The text defines deep models by their depth

stating

"The core idea of deep learning is that we can learn a deep model by introducing more layers... In this book

we use the term 'deep learning' to refer to the study of deep models." This directly links the concept of "deep" to the number of layers (specifically

hidden layers).

3. Stanford University. (n.d.). CS231n: Convolutional Neural Networks for Visual Recognition

Course Notes.

Module 1: Neural Networks Part 1: Setting up the Architecture: The notes explain the structure of neural networks

defining the input layer

hidden layer(s)

and output layer. It clarifies that a "deep" network is one with multiple hidden layers

distinguishing it from a "2-layer Net" (one hidden layer). This establishes that hidden layers are the components that create depth.

The Akaike Information Criterion (AIC) is the most suitable method for this task. AIC is a statistical estimator used for model selection that evaluates the relative quality of statistical models for a given set of data. It provides a means for model selection by estimating the trade-off between the goodness of fit of the model and its complexity (the number of parameters). When comparing a set of candidate models, including various nonlinear ones, the model with the lowest AIC value is preferred. This makes it an ideal tool for evaluating and comparing the performance of different model structures.

B. Chi-squared test: This test primarily assesses the goodness of fit of a single model or tests for independence between variables, not for comparing multiple, potentially non-nested models.

C. MCC: The Matthews Correlation Coefficient is a performance metric specifically for binary classification models, not a general tool for comparing various types of models as requested.

D. ANOVA: Analysis of Variance is typically used to compare the means of different groups or to compare nested linear models, making it less suitable for diverse nonlinear model comparison.

1. Hastie

T.

Tibshirani

R.

& Friedman

J. (2009). The Elements of Statistical Learning: Data Mining

Inference

and Prediction (2nd ed.). Springer. In Chapter 7

Section 7.5

"The Akaike Information Criterion

" pages 233-234

the text explains that AIC is a widely used criterion for model selection that trades off model fit with the number of parameters

making it suitable for comparing different models.

2. Burnham

K. P.

& Anderson

D. R. (2002). Model selection and multimodel inference: A practical information-theoretic approach (2nd ed.). Springer-Verlag. Chapter 2

Section 2.2

"Akaike's Information Criterion

" pages 60-66

details the application of AIC for selecting the best model from a set of candidates

emphasizing its utility in comparing models that may not be nested.

3. Pennsylvania State University. (n.d.). STAT 501: Regression Methods

Lesson 11: Model Selection & Validation. Eberly College of Science. In Section 11.2

"AIC

BIC

and Mallows' Cp

" the courseware describes AIC as an estimate of prediction error used to select the best model from a set of candidates

where the model with the lowest AIC is chosen.

The primary requirements are to model a non-linear phenomenon and maintain the highest possible degree of interpretability. A decision tree is the best choice as it naturally handles non-linear relationships by partitioning the feature space into distinct regions. Its hierarchical, rule-based structure (a series of if-then-else conditions) is highly intuitive and easy to visualize and explain to stakeholders. While other models can handle complexity, they sacrifice this crucial interpretability. A decision tree provides a clear, traceable path for each prediction, directly fulfilling the data scientist's main objective.

A. Artificial neural network: Fails the primary requirement for high interpretability; these are complex "black box" models whose internal logic is difficult to decipher.

C. Multiple linear regression: Is fundamentally unsuitable because the data scientist has already determined that no linear relationship exists between the predictors and the target.

D. Random forest: Is an ensemble of many decision trees, which significantly reduces interpretability compared to a single, well-defined tree.

1. James

G.

Witten

D.

Hastie

T.

& Tibshirani

R. (2013). An Introduction to Statistical Learning: with Applications in R. Springer. In Chapter 8

Section 8.1

"The Basics of Decision Trees

" the authors state

"Trees are very easy to explain to people... Some people believe that decision trees more closely mirror human decision-making than do the regression and classification approaches... The cost of a tree—that is

its complexity and interpretability—is governed by the number of splits it has." This highlights the direct link between a single tree and high interpretability.

2. Molnar

C. (2022). Interpretable Machine Learning: A Guide for Making Black Box Models Explainable. In Chapter 4.1

"Decision Tree

" it is noted

"The decision tree is one of the most interpretable models... The 'if-then' structure is intuitive for humans." The chapter contrasts this with the lack of interpretability in more complex models like neural networks and the reduced transparency of ensembles like random forests.

3. MIT OpenCourseWare. (2020). 6.036 Introduction to Machine Learning

Fall 2020. Lecture 9: Decision Trees. The course materials describe decision trees as a non-linear model class that is "very easy to interpret" by following the path from the root to a leaf node

which directly corresponds to a set of rules. This is contrasted with ensembles

which gain predictive power at the cost of this direct interpretability.